柏林噪声算法解析

柏林噪声（Perlin Noise）算法是 Ken Perlin 发明的一种自然噪声生成算法，并在图形学领域广泛使用。例如模拟火焰、云彩的纹理、生成随机地形图等。

案例分析

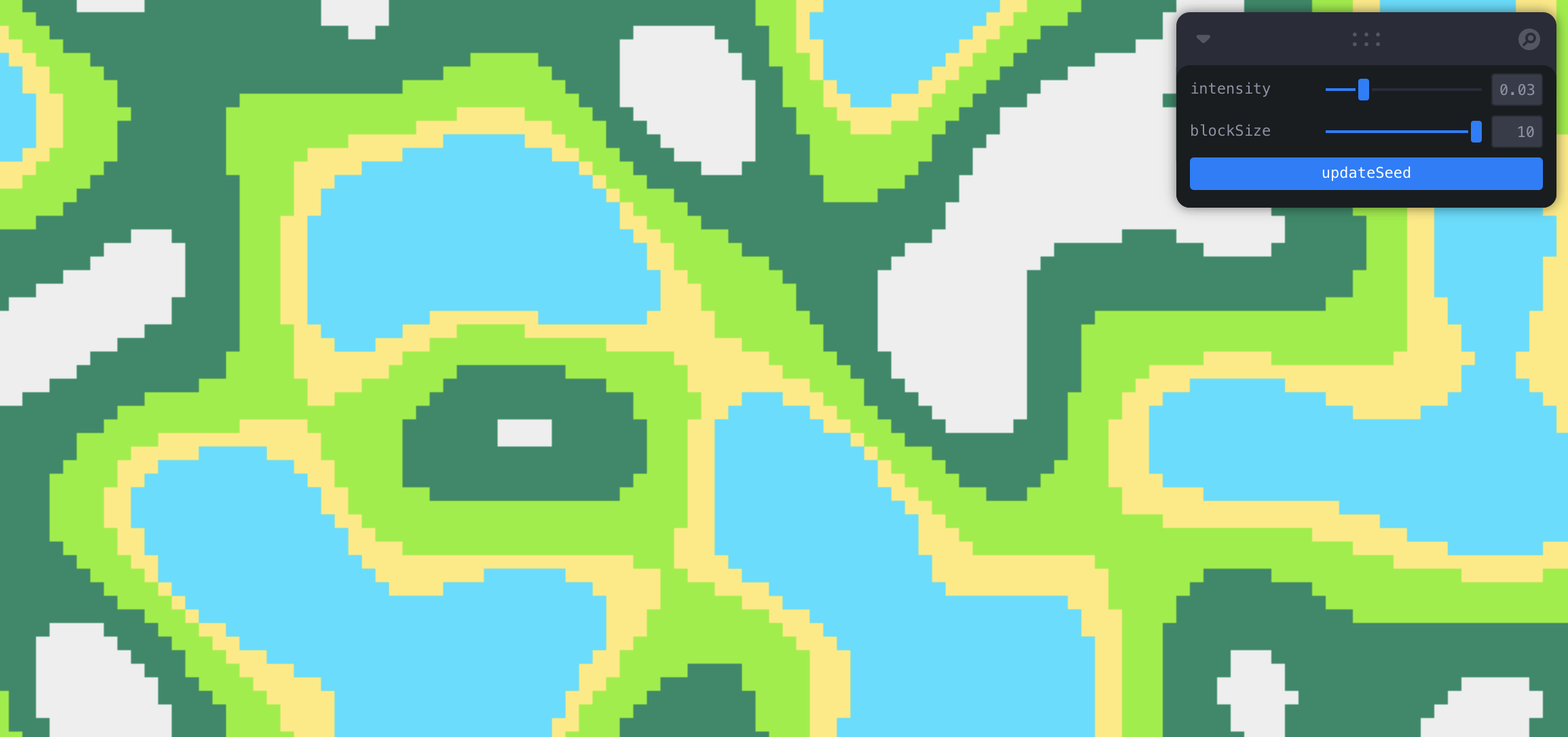
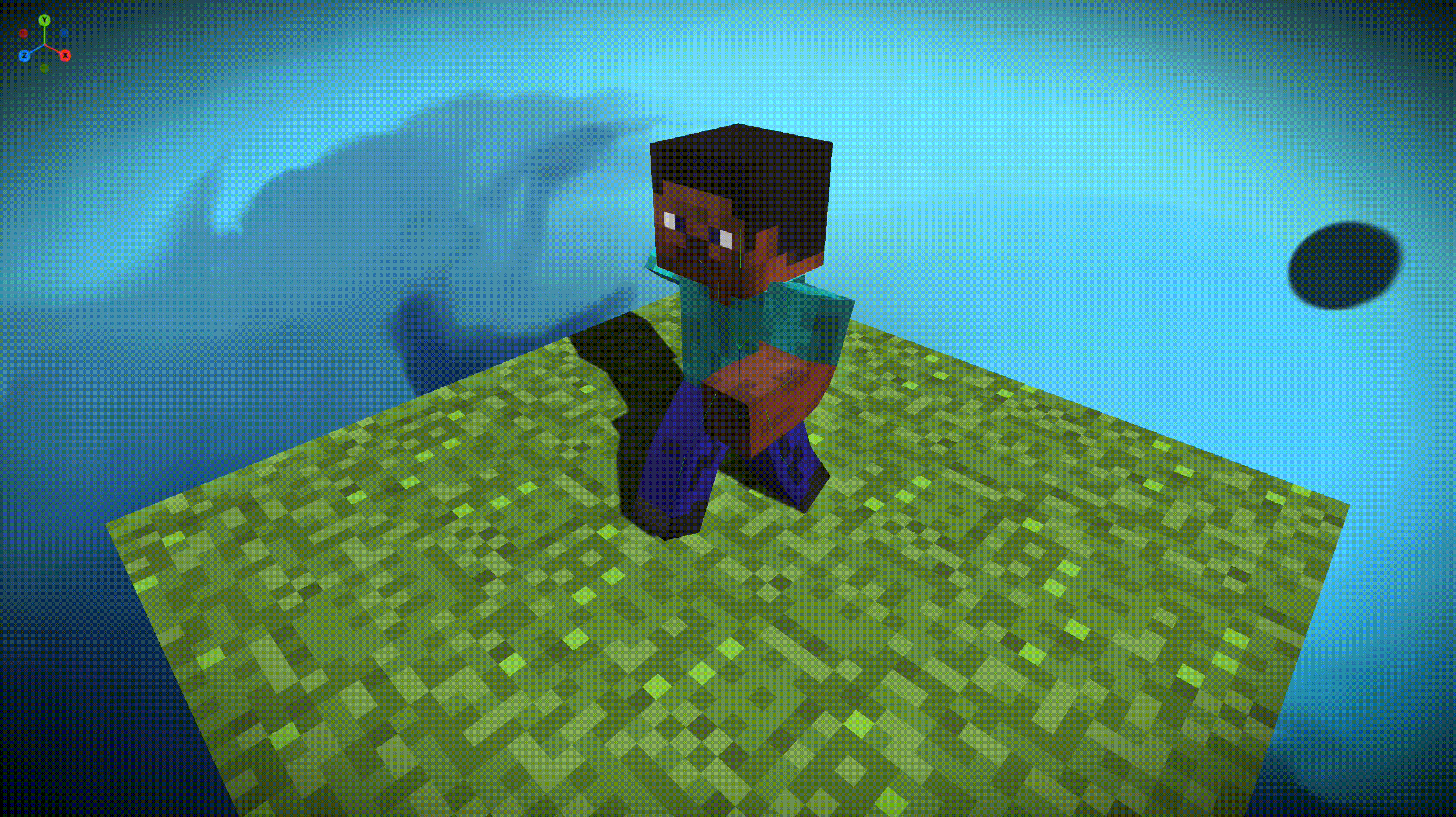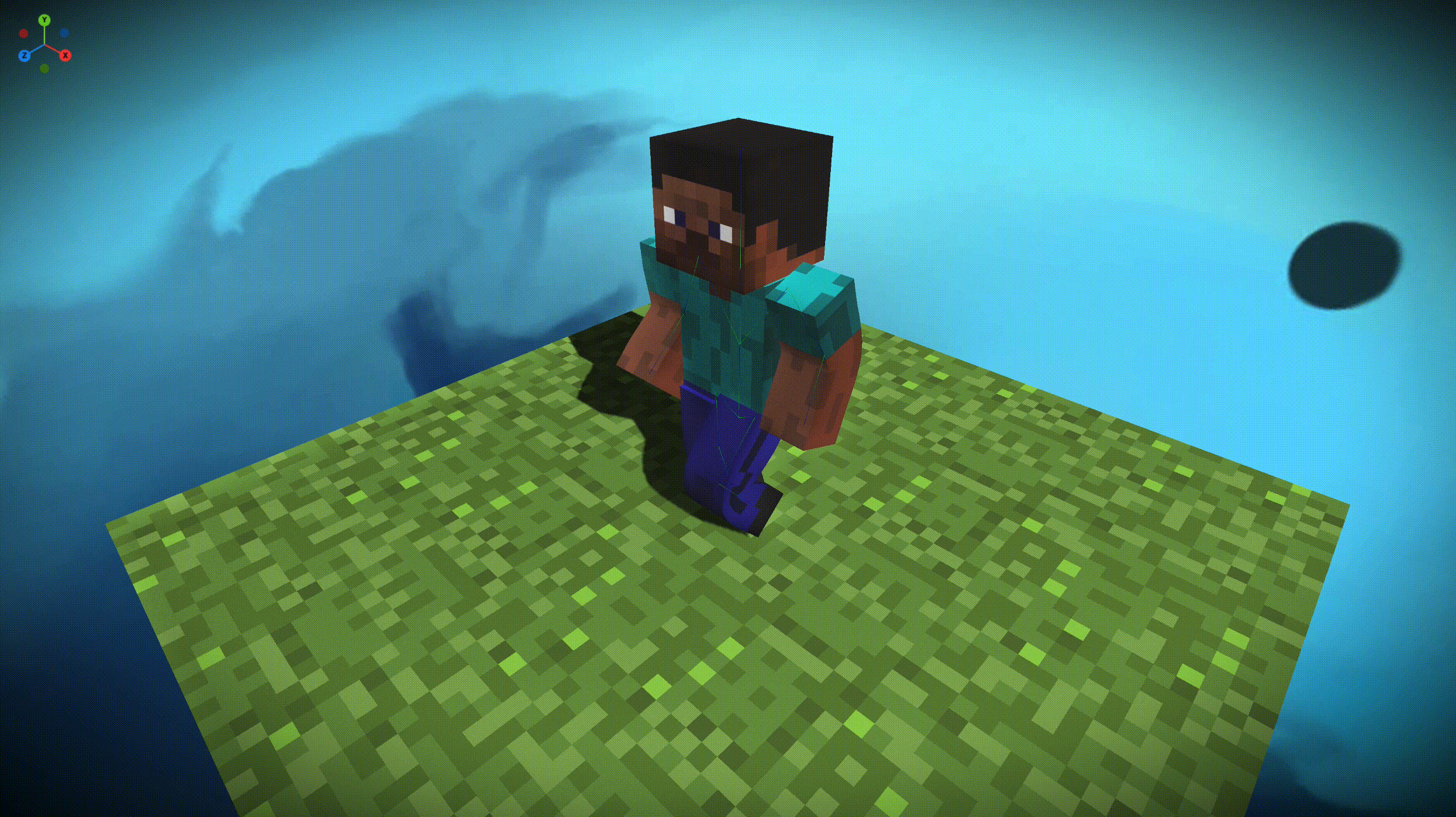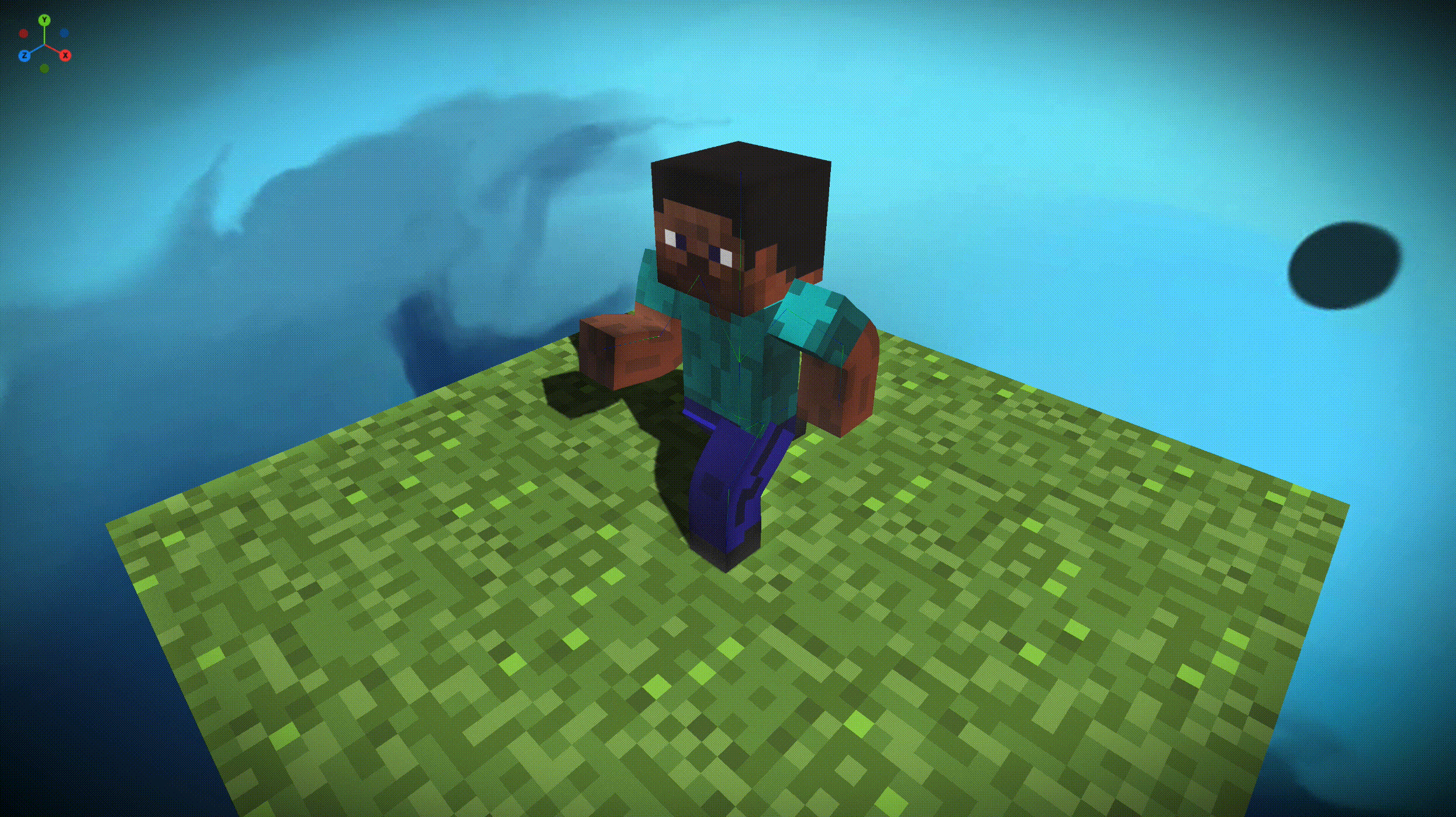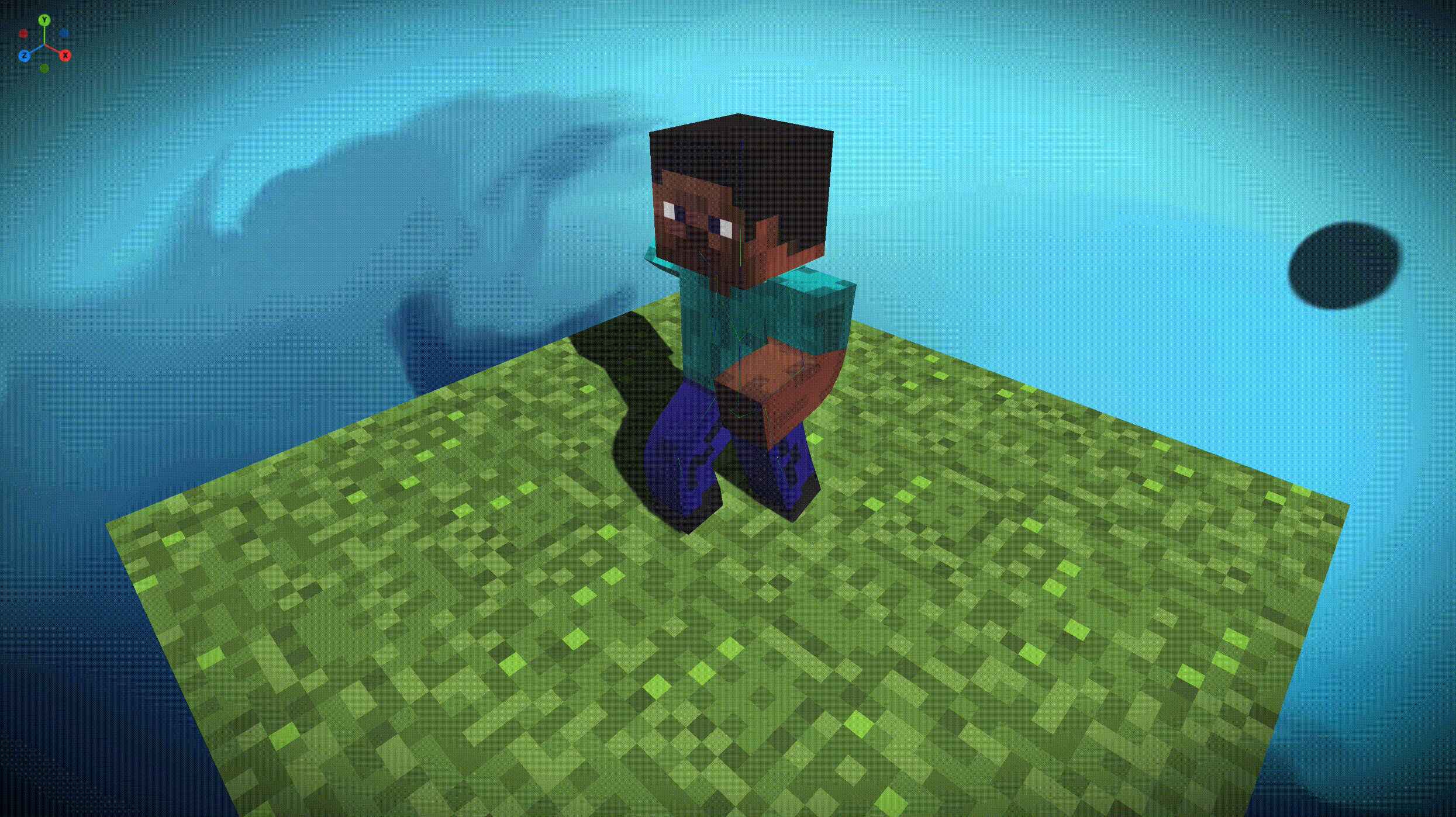
封面图是我利用柏林噪声实现的地图生成器。以下是绘制逻辑的主要代码，

for (let x = 0; x < xMax; x++) {
  for (let y = 0; y < yMax; y++) {
    const v = noise(x, y);
    if (v > 0.8) {
      drawBlock(x, y, '#eeeeee') // 海洋
    } else if (v > 0.6) {
      drawBlock(x, y, '#168B67') // 沙地
    } else if (v > 0.4) {
      drawBlock(x, y, '#88F116') // 平原
    } else if (v > 0.3) {
      drawBlock(x, y, '#FFEB79') // 高原
    } else {
      drawBlock(x, y, '#2EDFFF') // 雪山
    }
  }
}

首先我把屏幕区域按照 BlockSize 分成 [xMax, yMax] 数量的区块，通过柏林噪声生成一张二维连续的高度图，noise(x, y) 取到高度值，根据高度值将 BlockType 划分为：海洋、沙地、平原、高原、雪山，然后给区块着色。

算法分析

由以上案例可知，当入参 (x, y) 连续，noise(x, y) 的值也是连续的，那么 noise 函数是如何实现的呢？柏林噪声是一种 基于晶格的 (Lattice based) 梯度噪声算法(Gradient Noise)。下面是算法解析：

划分晶格

我们暂且以长度为 1 的晶格划分整个二维空间，如下图，当我们的入参 (x, y) 为 (3.7, 2.7) 时，坐标点将落入右侧的正方形晶格中。

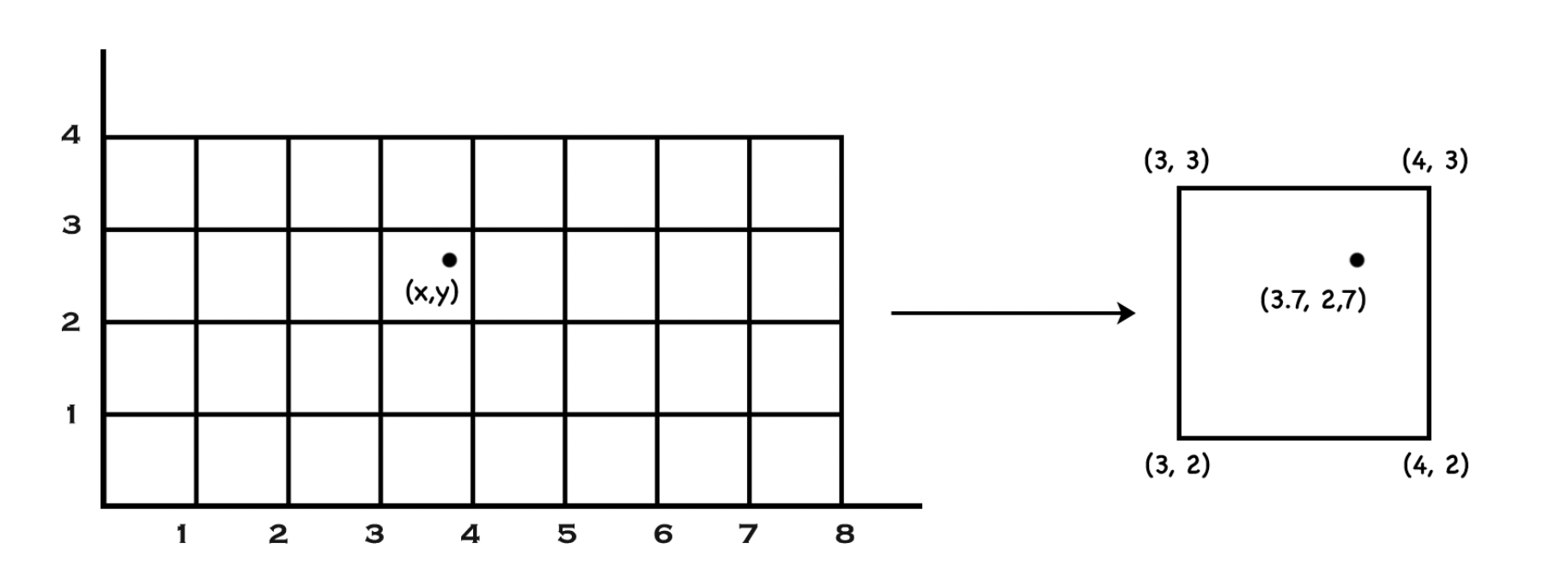
梯度向量

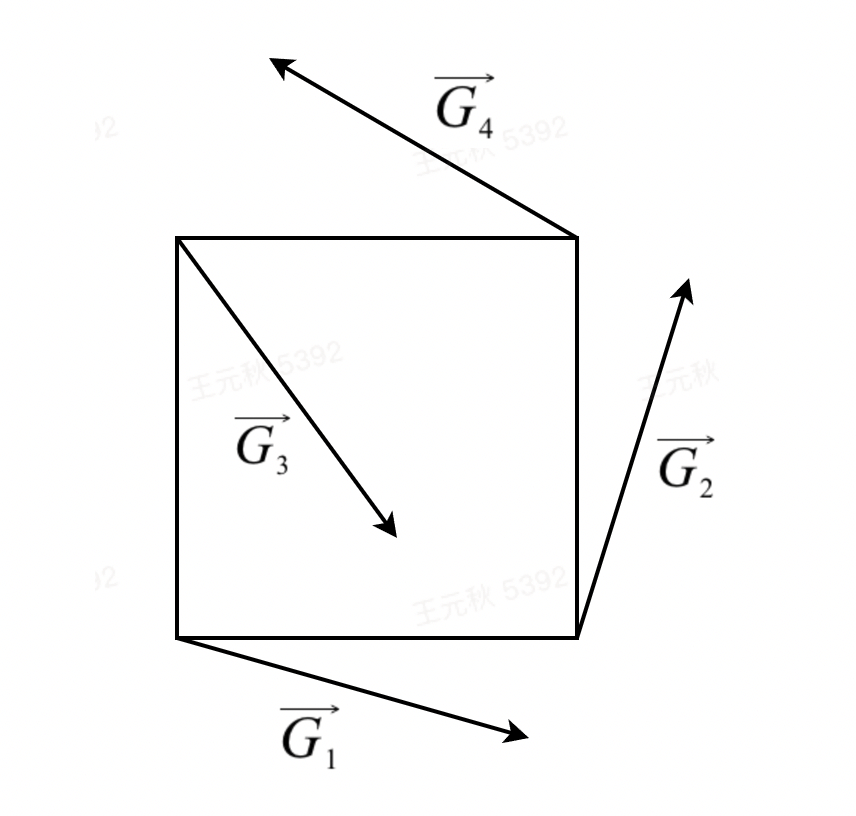
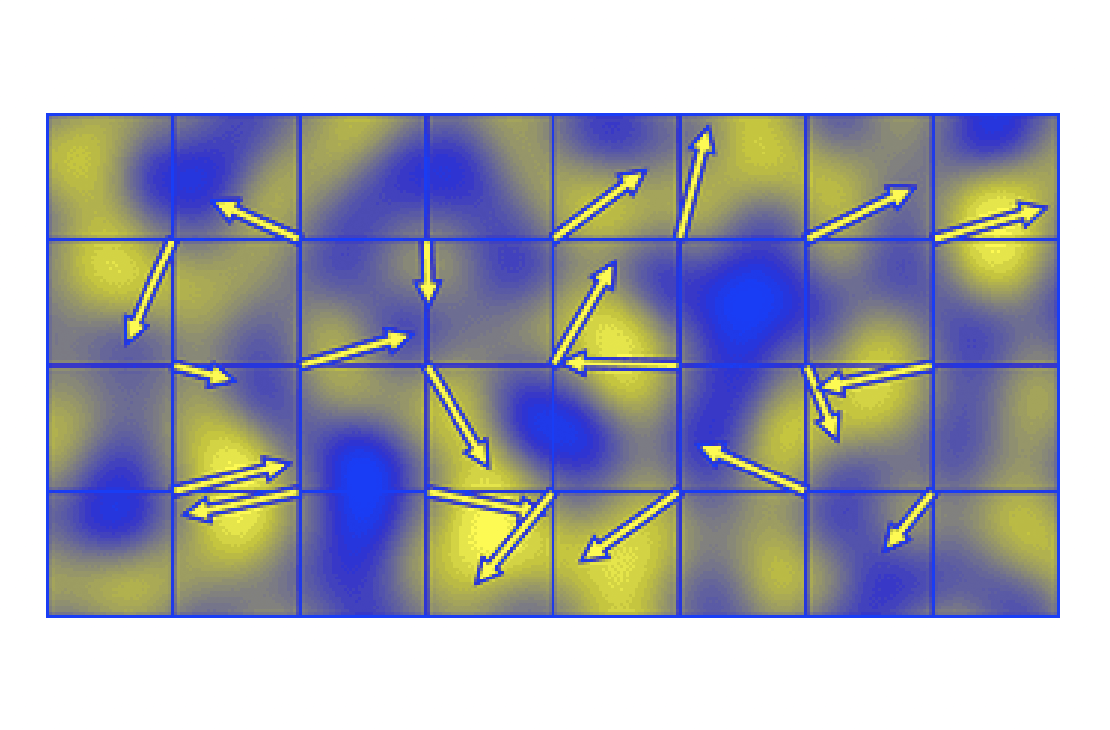
然后我们分别以正方形的 4 个晶格为原点，各自生成一个 伪随机 的梯度向量，如下面左图中的 G1、G2、G3、G4。顶点的梯度向量代表 该顶点对于晶格内点的 影响 。 伪随机的含义是当 seed 一定时，梯度向量也相同。

打个简单的比方，晶格空间内原本分布着均匀的像素点，这时候四个顶点分别有 4 个沿着向量方向的力进行拉扯，沿着力的方向像素点越密集，就像右上这样，越接近黄色的区域，空间分布越密集，影响值越大。

距离向量

怎么去量化这种 影响 呢？我们引入距离向量。如下图所示，对于空间内的点 P(x, y)，四个顶点分别生成了指向它的距离向量 D1、D2、D3、D4。

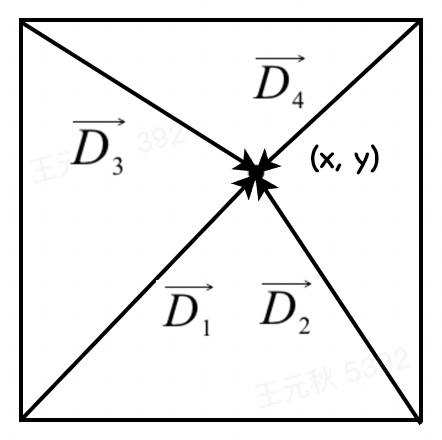
顶点对该点的影响值即为梯度向量 G 与距离向量 D 的点积。由此我们得到：

$$
\begin{cases}
u_1 = \overrightarrow {G_1} \centerdot \overrightarrow {D_1} \\
u_2 = \overrightarrow {G_2} \centerdot \overrightarrow {D_2} \\
u_3 = \overrightarrow {G_3} \centerdot \overrightarrow {D_3} \\
u_4 = \overrightarrow {G_4} \centerdot \overrightarrow {D_4}
\end{cases}
$$

归一化处理

我们现在得到了 4 个标量 u1、u2、u3、u4，且都随变量 P(x, y) 连续变化，现在我们需要将他们合并成一个值 t，使得 t 同样随着 P(x, y) 连续变化。

$$
t_1 = lerp(u_1, u_2, x)
$$

$$
t_2 = lerp(u_3, u_4, x)
$$

$$
t = lerp(t_1, t_2, y)
$$

插值函数

上面公式中提到的 lerp 函数就是插值函数，其实在我们日常编码中经常会使用到，例如 css 的 transition-timing-function 的属性 linear、ease、ease-in、ease-out、ease-in-out 等等都是插值函数。他们的函数图像如下：

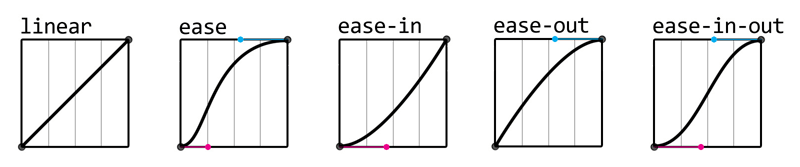
拿最简单的线性插值函数为例，实现代码如下：

const lerp = (min, max, t) => min * (1 - t) + max * t;

至此，我们根据传入点 (x, y) 通过算法 Perlin(x, y) 得到了一个归一化的结果 t，并且结果 t 会随着 (x, y) 的变化而连续变化，这就是柏林噪声算法。具体实现代码因为篇幅原因我就不贴出来了，感兴趣的同学可以根据上述分析自己实现一下。